Circles ⇒⇒ Exercise 9.3

Question 1

In the given figure, A, B, and C are three points on a circle with centre O such that $ \angle $ BOC = 30° and $ \angle $ AOB = 60°. If D is a point on the circle other than the arc ABC, find $ \angle $ ADC.

Solution :

Given, a circle with centre O, such that $ \angle $ AOB = 60° and $ \angle $ BOC = 30°

$ \angle $ ADC = ?

$ \angle $ AOC = $ \angle $ AOB + $ \angle $ BOC

( Given $ \angle $ AOB = 60° and $ \angle $ BOC = 30° )

$ \angle $ AOC = 60° + 30°

∴ $ \angle $ AOC = 90°

The theorem states that the angle subtended by an arc at the center is double the angle subtended by the same arc at any point on the remaining part of the circle.

The arc ABC subtends $ \angle $ AOC at the center O. Since D is a point on the circle other than the arc ABC,

$ \angle $ ADC is the angle subtended by the arc AC on the remaining part of the circle.

$ \angle $ ADC = 1/2 × $ \angle $ AOC

⇒ $ \angle $ ADC = 1/2 × 90°

⇒ $ \angle $ ADC = 45°

Question 2

A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

Solution :

Given: A chord of a circle is equal to the radius of the circle

To find: $ \angle $ MAN = ? and $ \angle $ MQN = ?

Let OM and ON be the two radii of the circle and let MN be the chord equal to the length of radius. i.e. OM = ON = MN .

Join them to form a triangle.

Therefore, the triangle △OMN is an equilateral triangle because all its sides are equal.

( Each angle in equilateral triangle is equal to 60° )

∴ angle subtended at the centre $ \angle $ MON = 60°

Now, It is known that,The angle subtended by an arc at any point on the remaining part of the circle (the major arc) is half the angle subtended by it at the center.

∴ Angle subtended at point A on the circle

$ \angle $ MAN = 1/2 × $ \angle $ MON

⇒ $ \angle $ MAN = 1/2 × 60°

⇒ $ \angle $ MAN = 30°

The points A, M,Q, and a point N on the minor arc form a cyclic quadrilateral AMQN.

Now, In cyclic quadrilateral AMQN,

( The sum of either pair of opposite angles of a cyclic quadrilateral is 180° )

∴ $ \angle $ MAN + $ \angle $ MQN = 180°

⇒ 30° + $ \angle $ MQN = 180°

⇒ $ \angle $ MQN = 180° - 30°

⇒ $ \angle $ MQN = 150°

(i) Hence, the angle subtended by the chord on the major arc , $ \angle $ MAN = 30°

(ii)And, the angle subtended by the chord on the minor arc, $ \angle $ MQN = 150°

Question 3

In the given figure, $ \angle $ PQR = 100°. Where P, Q and R are points on a circle with centre O. Find $ \angle $ OPR.

Solution :

Given, a circle with centre O, such that $ \angle $ PQR = 100°

To find: $ \angle $ OPR = ?

We know that, The angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.

∴ Reflex angle $ \angle $ POR = 2 $ \angle $ PQR

( By degree measure theorem, )

= 2 × 100°

= 200°

Now , $ \angle $ POR

The interior angle $ \angle $ POR is found by subtracting the reflex angle from 360° :

$ \angle $ POR + Reflex $ \angle $ POR = 360°

( Complete angle )

⇒ $ \angle $ POR = 360° - 200°

⇒ $ \angle $ POR = 160°

Now , In triangle POR

OP = OR

( Radii of a circle )

Since two sides are equal, △POR is an isosceles triangle.

$ \angle $ OPR = $ \angle $ ORP

( The angles opposite the equal sides must also be equal )

∴ $ \angle $ OPR + $ \angle $ ORP + $ \angle $ POR = 180°

( Sum of all angles in a triangle is 180° )

⇒ $ \angle $ OPR + $ \angle $ OPR + 160 = 180°

⇒ 2 $ \angle $ OPR + 160° = 180°

⇒ 2 $ \angle $ OPR = 180° - 160°

⇒ 2 $ \angle $ OPR = 20°

⇒ $ \angle $ OPR = 10°

Therefore, $ \angle $ OPR = 10°

Question 4

In the given figure, $ \angle $ ABC = 69°, $ \angle $ ACB = 31°, find $ \angle $ BDC.

Solution :

Given, a circle with centre O, such that $ \angle $ ABC = 69° and $ \angle $ ACB = 31°

To find: $ \angle $ BDC = ?

In triangle ABC

$ \angle $ ABC + $ \angle $ ACB + $ \angle $ BAC = 180°

( Angle Sum Property of a Triangle, Sum of all angles in a triangle is 180° )

⇒ 69° + 31° + $ \angle $ BAC = 180°

( Given, $ \angle $ ABC = 69° and $ \angle $ ACB = 31° )

⇒ $ \angle $ BAC + 100° = 180°

⇒ $ \angle $ BAC = 180° - 100°

⇒ $ \angle $ BAC = 80°

The $ \angle $ BDC and the $ \angle $ BAC are both subtended by the same arc, arc BC, at the circumference.

$ \angle $ BDC = $ \angle $ BAC

( According to the Angles in the Same Segment Theorem, angles subtended by the same arc (or chord) in the same segment of a circle are equal. )

∴ $ \angle $ BDC = $ \angle $ BAC = 80°

$ \angle $ BDC = 80°

Question 5

In the given figure, A, B, C, and D are four points on a circle. AC and BD intersect at a point E such that $ \angle $ BEC = 130° and $ \angle $ ECD = 20°. Find $ \angle $ BAC.

Solution :

Given, A, B, C and D are four points on a circle, such that $ \angle $ BEC = 130° and $ \angle $ ECD = 20°

To find: $ \angle $ BAC = ?

AC and BD are intersecting lines. $ \angle $ BEC and $ \angle $ DEC form a linear pair on the line BD.

$ \angle $ BEC + $ \angle $ DEC = 180°

( The sum of two adjacent angles is 180° ,Linear pair )

∴ 130° + $ \angle $ DEC = 180°

⇒ $ \angle $ DEC = 180° - 130°

⇒ $ \angle $ DEC = 50°

Consider Now in Δ DEC

$ \angle $ DEC + $ \angle $ ECD + $ \angle $ EDC = 180°

( The sum of interior angles of a triangle is 180° )

⇒ 50° + 20° + $ \angle $ EDC = 180°

( Given, $ \angle $ ECD = 20° and proved above $ \angle $ DEC = 50° )

⇒ 70° + $ \angle $ EDC = 180°

⇒ $ \angle $ EDC = 180° - 70°

⇒ $ \angle $ EDC = 110°

Since Δ BAC and Δ BDC are at same arc, so

$ \angle $ BDC = $ \angle $ BAC

( According to the Angles in the Same Segment Theorem, angles subtended by the same arc (or chord) in the same segment of a circle are equal. )

∴ $ \angle $ BDC = $ \angle $ BAC = 110°

( Proved above $ \angle $ EDC = $ \angle $ BDC = 110° )

$ \angle $ BAC = 110°

Question 6

ABCD is a cyclic quadrilateral whose diagonals intersect at a point E . If $ \angle $ DBC = 70°, $ \angle $ BAC = 30°, find $ \angle $ BCD. Further, if AB = BC, find $ \angle $ ECD.

Solution :

Given, A, B, C and D are four points on a circle, such that $ \angle $ DBC = 70° and $ \angle $ BAC = 30°

And, AB = BC

To find: $ \angle $ ECD = ?

Since Δ CAD and Δ CBD are at same arc, so

$ \angle $ CAD = $ \angle $ DBC

( The Angles in the Same Segment Theorem states that angles subtended by the same arc at the circumference are equal.. )

∴ $ \angle $ CAD = $ \angle $ DBC = 70°

( Given $ \angle $ DBC = 70° )

$ \angle $ CAD = 70°

Now, in cyclic quadrilateral ABCD,

( The sum of either pair of opposite angles of a cyclic quadrilateral is 180° )

∴ $ \angle $ BCD + $ \angle $ BAD = 180°

⇒ $ \angle $ BCD + ($ \angle $ BAC + $ \angle $ CAD ) = 180°

( ∵ $ \angle $ BAD = $ \angle $ BAC + $ \angle $ CAD )

⇒ $ \angle $ BCD + (30° + 70° ) = 180°

( Given, $ \angle $ BAC = 30° and proved above $ \angle $ CAD = 70° )

⇒ $ \angle $ BCD + 100° = 180°

⇒ $ \angle $ BCD = 180° - 100°

⇒ $ \angle $ BCD = 80°

Consider Now in Δ ABC

AB = BC

∴ $ \angle $ BAC = $ \angle $ BCA

( Angles opposite to equal sides of a triangle )

$ \angle $ BAC = $ \angle $ BCA = 30°

$ \angle $ BCA = 30°

∴ $ \angle $ ECD = $ \angle $ BCD – $ \angle $ BCA

$ \angle $ ECD = 80° – 30°

$ \angle $ ECD = 50°

Thus, the value of $ \angle $ ECD is 50°

Question 7

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Solution :

Let A, B, C and D are four vertices of cyclic quadrilateral ABCD on a circle, and the diagonals AC and BD are the diameters, intersecting each other at point O

To Prove: ABCD is a rectangle

Given here AC be the diameter of the circle which is also a chord, so

⇒ $ \angle $ ADC = 90°

Similarly, $ \angle $ ABC = 90°

( Angle in a Semicircle Theorem, which states that the angle subtended by a diameter at any point on the circumference is a right angle 90° )

Now considering here, BD be the diameter of the circle which is also a chord, so

⇒ $ \angle $ BAD = 90°

Similarly, $ \angle $ BCD = 90°

( Angle in a Semicircle Theorem, which states that the angle subtended by a diameter at any point on the circumference is a right angle 90°)

Now, four angles of quadrilateral ABCD are right angles.

$ \angle $ A =$ \angle $ B = $ \angle $ C =$ \angle $ D = 90°

Each interior angle in quadrilateral ABCD is 90°

∴ ABCD is a rectangle.

Question 8

If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Solution :

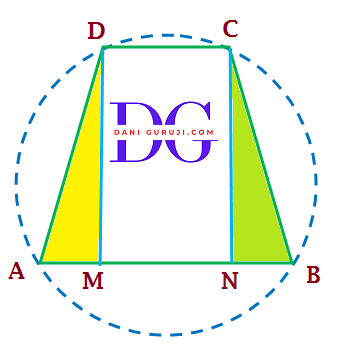
Let A, B, C and D are four vertices of trapezium ABCD , and the parallel lines are AB, DC and the non parallel lines AD and BC are equal.

AB || CD and AD = BC

To Prove: ABCD is a cyclic trapezium.

Construction : Draw DM perpendicular to AB and CN perpendicular to AB

In ΔAMD and ΔBNC,

AD = BC

( Given AD = BC )

$ \angle $ AMD = $ \angle $ BNC

( By construction each angle is 90° )

DM = CN

( Perpendicular distance between two parallel lines is same )

Thus , ΔAMD and ΔBNC are congruent

( By RHS congruence rule )

Therefore,

$ \angle $ DAM = $ \angle $ CBN Or $ \angle $ A = $ \angle $ B

and $ \angle $ ADM = $ \angle $ BCN

( By CPCT )

A quadrilateral is cyclic if its opposite angles are supplementary. We need to prove $ \angle $ A+ $ \angle $ C = 180° or $ \angle $ B + $ \angle $ D = 180° .

Now,

⇒ $ \angle $ ADM + 90° = $ \angle $ BCN + 90°

⇒ $ \angle $ ADM + $ \angle $ MDC = $ \angle $ BCN + $ \angle $ NCD

( By construction $ \angle $ MDC = $ \angle $ NCD = 90° )

⇒ $ \angle $ ADC = $ \angle $ BCD

⇒ $ \angle $ D = $ \angle $ C

Now,

$ \angle $ A = $ \angle $ B and $ \angle $ D = $ \angle $ C

∴ $ \angle $ A + $ \angle $ B + $ \angle $ D + $ \angle $ C = 360°

( ∵ Sum of the angles of a quadrilateral is 360° )

⇒ 2$ \angle $ B + 2$ \angle $ D = 360°

⇒ $ \angle $ B + $ \angle $ D = 180°

( A pair of opposite angles of quadrilateral is 180° )

This equation proves that the opposite angles are supplementary.

Hence, ABCD is a cyclic trapezium.

Question 9

Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively(see Fig below) . Prove that$ \angle $ ACP =$ \angle $ QCD.

Solution :

To Prove:$ \angle $ ACP =$ \angle $ QCD

Construction : Join chords AP and DQ

Since Δ ACP and Δ PBA are at same chord AP, so

$ \angle $ ACP =$ \angle $ PBA .....(i)

( We know that, angles in the same segment of a circle are equal )

Now, Since Δ DBQ and Δ DCQ are at same chord DQ, so

$ \angle $ DBQ =$ \angle $ QCD .....(ii)

( We know that, angles in the same segment of a circle are equal )

Now,

ABD and PBQ are line segments intersecting at point B

$ \angle $ PBA =$ \angle $ DBQ .....(iii)

( Vertically opposite angles )

From equation (i) (ii) and (iii), we get

$ \angle $ ACP =$ \angle $ QCD

Hence proved.

Question 10

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Solution :

Two circles are drawn taking CA and CB of a triangle as diameter.

Let these circles intersect at point C and D.

To Prove: that point of intersection of the two circles 'D' lie on the third side AB of ∆ABC.

Construction : Join CD

Proof: AC is the diameter of the circle and $ \angle $ ADC is formed in a semi-circle.

Then,

$ \angle $ ADC = 90° ......(i)

( We know that,Angle in a semicircle is a right angle )

Similarly, BC is the diameter of the circle and $ \angle $ BDC is formed in a semi-circle.

Then,

$ \angle $ BDC = 90° .....(ii)

( We know that,Angle in a semicircle is a right angle )

Adding (i) and (ii), we get

$ \angle $ ADC + $ \angle $ BDC = 90° + 90°

$ \angle $ ADB = 180°

Since $ \angle $ ADB = 180° the points A, D, and B are collinear (lie on the same straight line).

Then, ADB is a straight line.

Because D lies on the line segment AB and is distinct from A and B, the point of intersection D must lie on the third side AB of the triangle.

Hence Proved.

Question 11

∆ ABC and ∆ ADC are two right triangles with common hypotenuse AC. Prove that $ \angle $ CAD = $ \angle $ CBD.

Solution :

We have right ∆ ABC and ∆ ADC such that they are having AC as their common hypotenuse.

So, $ \angle $ B = $ \angle $ D = 90°.

To Prove: $ \angle $ CAD = $ \angle $ CBD.

Construction : Join BD

Given: $ \angle $ ABC and $ \angle $ ADC are 90° .

Then,

$ \angle $ ABC + $ \angle $ ADC = 90°+ 90° = 180°

( We know that, A pair of opposite angles of a cyclic quadrilateral is 180° )

Hence, ABCD is the cyclic quadrilateral.

Now here, Δ CAD and Δ CBD are at same arc CD , so

∴ $ \angle $ CAD = $ \angle $ CBD

( We know that, angles in the same segment of a circle are equal. )

Hence Proved.

Question 12

Prove that a cyclic parallelogram is a rectangle.

Solution :

Let ABCD be the cyclic parallelogram.

To Prove: ABCD is a rectangle.

$ \angle $ A = $ \angle $ C and $ \angle $ B = $ \angle $ D .... (i)

( We know that, opposite angles of a parallelogram are equal )

But,

$ \angle $ A + $ \angle $ C = 180°

( We know that, A pair of opposite angles of a cyclic quadrilateral is 180° )

From equation (i)

$ \angle $ A + $ \angle $ A = 180°

$ \angle $ A = 90°

We know that if one of the interior angles of a parallelogram is 90° .

All the other angles will also be equal to 90° .

If each angle of the parallelogram is a right angle, it is a rectangle.

Hence, ABCD is a rectangle.

Hence Proved.